PERPENDICULARES

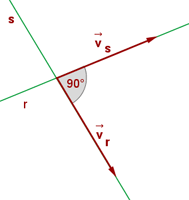
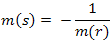Podemos afirmar que dos rectas son perpendiculares cuando forman exactamente 90° al intersectarse o cortarse.

Las pendientes de rectas perpendiculares son inversas y de signo contrario.

PARALELAS

Dos rectas son paralelas cuando van a mantener la misma distancia de separación.

Para el matemático y filósofo Euclídes las rectas paralelas nunca se cortan entre sí.

Otros estudios avanzados de geometría han cuestionado lo que afirmaba Euclídes.

Para la Geometría Analítica dos rectas que son paralelas van a tener la misma pendiente.

M1  = M2

PARALELISMO Y PERPENDICULARIDAD

PARALELISMO:

   Dos rectas son paralelas si sus vectores directores sonparalelos, es decir, si     éstos son linealmente dependientes.

     

    Dos rectas son paralelas si:

•  Sus vectores directores son iguales 
•  Sus pendientes son iguales
•  Los coeficientes de x e y respectivos son proporcionales
•  Forman un ángulo de 0º

    EJEMPLO: Calcular una recta paralela a r ≡ x + 2 y + 3 = 0, que pasen por                                          el punto A(3,5).

     

PERPENDICULARIDAD:

   Dos rectas son perpendiculares si sus vectores directores son perpendiculares.

      

   Si dos rectas son perpendiculares tienen sus pendientes inversas y cambiadas de signo.

   EJEMPLO: Calcular una recta perpendicular a r ≡ x + 2 y + 3 = 0, que pasen por el punto A(3,5).

  

TERCER FORMA DE LA ECUACIÓN LINEAL

Esta forma también recibe el nombre de FORMA REDUCIDA

Consiste en obtener a la ecuación igual a 1.

Ejemplo:

5x- 2y =6 5x /6 - 2y/6 = 6/65/6 x - 2/6 y = 1 

PENDIENTE Y ORDENADA AL ORIGEN

Utilizamos la fórmula:

Y = mx + b 

Para graficar esta forma se aplica el método ABSCISA Y ORDENADA AL ORIGEN.

FORMAS DE LA ECUACIÓN LINEAL

PUNTO - PENDIENTE

Para aplicar esta forma requerimos las coordenadas de un punto y la pendiente de la recta.

En caso de que no tengamos la pendiente se hace necesario tener 2 coordenadas que formen a esa recta.

ELEMENTOS DE UNA ECUACIÓN LINEAL O DE PRIMER GRADO

FORMA GENERAL DE UNA ECUACIÓN LINEAL:

Ax + By + C = O 

Ax = término lineal en X

By= término lineal en Y

C= término independiente

Forma pendiente ordenada el origen

Pendiente Ordenada el origen

ABSCISA Y ORDENADA EN EL ORIGEN

Existe un método para graficar a una recta que se llama ABSCISA Y ORDENADA EN EL ORIGEN
Este consiste en primer lugar en despejar cada uno de las variables.
Para poderlo hacer primeramente se le asigna a "X" el valor de 0 y posteriormente a "Y"