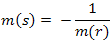En general

ECUACIÓN DE LA PARÁBOLA

ECUACIONES DELA PARÁBOLA CON VÉRTICE EN EL ORIGEN

PRIMER CASO:

EL vértice está en el origen y la parábola abre hacia la derecha.

FORMULA. y2 =4px

P= distancia focal ó eje focal

Lr=4p

SEGUNDO CASO:

El vértice está en el origen y la parábola abre a la izquierda.

FÓRMULA : y2 = -4 px

TERCER CASO:

La parábola abre hacia arriba.

FÓRMULA: x2 = 4 py

CUARTO CASO:

La parábola abre hacia abajo.

FÓRMULA:   x2 = -4py

PASOS PARA GRAFICAR

1.Escribe tu ecuación en el papel.

2.Reorganiza la ecuación en la forma de una parábola, si es necesario. Recuerda la ecuación: y - k = a (x - h) ^ 2. Nuestro ejemplo es y - 3 = - 1/6 (x + 6) ^ 2, donde ^ denota un exponente.

3.Encuentra el vértice de la parábola. El vértice es el centro exacto de la parábola, el componente clave.

4.Utilizando la fórmula de una parábola, y - k = a (x - h) ^ 2, el vértice de la coordenada x (horizontal) es "h" y de la coordenada y (vertical) es "k".

5.Encuentra estos dos valores en la ecuación actual. Nuestro ejemplo es h = - 6 y k = 3.

vEncuentra el punto de intersección resolviendo la ecuación de "y". Ajusta "x" a "0" y despeja "y". En nuestro ejemplo y = -3

vEncuentra la intersección x resolviendo la ecuación de "x". Ajusta "y" a "0" y despeja "x". Cuando se toma la raíz cuadrada de ambos lados, el único número de la ecuación se convierte en positivo y negativo (+ / -), resultando en dos soluciones separadas, una utilizando el signo positivo y una el negativo.

vDibuja un gráfico, determina el tamaño y el área de la gráfica.

vTraza la parábola en la gráfica lineal.

TABULACIÓN DE LA PARÁBOLA POR TABULACIÓN

ELEMENTOS DE LA PARÁBOLA

-Directriz: La Directriz es la recta sobre la cual si medimos su distancia hasta un punto cualquiera de la parábola, esta debe ser igual a la distancia de este mismo punto al Foco

-Eje Focal: El eje focal es la recta perpendicular a la directriz que pasa por el foco. 

Ø  Vértice: Es el punto en el cual la parábola corta el eje focal. 

Ø  Lado Recto: Es un segmento paralelo a la directriz, que pasa por el foco y es perpendicular al eje focal y sus extremos son puntos de la parábola (A,B). 

Ø  Parámetro : La distancia entre el vértice y la directriz que es la misma entre el vértice y el foco de una parábola recibe el nombre de parámetro de la parábola (suele denotarse por p).

DEFINICIÓN COMO LUGAR GEOMÉTRICO

Son puntos que se mueven en el plano, de tal manera que está siempre a la misma distancia de un punto fijo llamado foco y de una recta llamada directriz, situados en un mismo plano.

UNIDAD 4 .PARÁBOLA

SECCIONES CÓNICAS

ECUACIÓN DE LA CIRCUNFERENCIA CON CENTRO FUERA DEL ORIGEN

En este caso vamos a resolver nuestros problemas utilizando la siguiente formula:

(x-h)2 + (y-k)2 = raiz de r2

Las literales h y k son las coordenadas del centro de la circunferencia

TERCER CASO DE LA CIRCUNFERENCIA

Nos proporciona centro en el origen y dos puntos que van a ser el diametro

En este caso podemos hacer 2 soluciones o caminos:

1.- Obtener el punto medio que su resultado debe ser C (0,0)

2.- Obtener el valor del radio como en el segundo caso

SEGUNDO CASO DE LA CIRCUNFERENCIA

A partir del centro y un punto por donde pasa la circunferencia (el centro está en el origen)

En este caso se ubica el centro y el punto dado en un plano cartesiano, posteriormente se obtiene la distancia del centro al punto (va a ser el radio)

Con el radio aplicamos la formula X 2 + Y2 = r2

Finalmente se obtiene la ecuación

EJEMPLO DE LA ECUACIÓN DE LA CIRCUNFERENCIA CON CENTRO EN EL ORIGEN

ECUACIÓN DE LA CIRCUNFERENCIA CON CENTRO EN EL ORIGEN

En ese caso la abscisa y la ordenda del centro de la circunferencia se encuentran en el origen, solamente debemos conocer el valor del radio.
Si nos proporcionan el diametro obtenemos la mitad:

CÍRCULO

Superficie plana limitada por una linea curva llamada CIRCUNFERENCIA.

Figura geométrica que consta de una forma establecida a partir de una línea curva cerrada

FORMULA PARA CALCULAR EL ÁREA: A= 3.14 X r2

CARACTERÍSTICAS:

> Sector circular
>Semi circulo
>Segmento circular
>Zona circular
>Corona circular
>Trapecio circular

Circunferencia

Es una línea curva cerrada, cuya característica principal es que todos los puntos equidistan de otro punto fijo llamado centro.

Una circunferencia está determinada por el centro y el radio de la misma.

Unidad III : "LA CIRCUNFERENCIA"

APLICACIONES DE LA RECTA EN LA VIDA COTIDIANA

-Medir distancias cortas entre dos puntos.
-Croquis.
-Plano cartesiano.
-Construcción de edificios.
-Resbaladillas.
-Instrumentos de medición: reglas, escuadras, etc
-Zapatos.
.Fotografías
-Dibujos

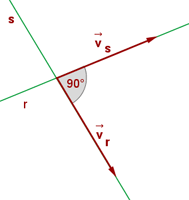
PERPENDICULARES

Podemos afirmar que dos rectas son perpendiculares cuando forman exactamente 90° al intersectarse o cortarse.

Las pendientes de rectas perpendiculares son inversas y de signo contrario.

PARALELAS

Dos rectas son paralelas cuando van a mantener la misma distancia de separación.

Para el matemático y filósofo Euclídes las rectas paralelas nunca se cortan entre sí.

Otros estudios avanzados de geometría han cuestionado lo que afirmaba Euclídes.

Para la Geometría Analítica dos rectas que son paralelas van a tener la misma pendiente.

M1  = M2

PARALELISMO Y PERPENDICULARIDAD

PARALELISMO:

   Dos rectas son paralelas si sus vectores directores sonparalelos, es decir, si     éstos son linealmente dependientes.

     

    Dos rectas son paralelas si:

•  Sus vectores directores son iguales 
•  Sus pendientes son iguales
•  Los coeficientes de x e y respectivos son proporcionales
•  Forman un ángulo de 0º

    EJEMPLO: Calcular una recta paralela a r ≡ x + 2 y + 3 = 0, que pasen por                                          el punto A(3,5).

     

PERPENDICULARIDAD:

   Dos rectas son perpendiculares si sus vectores directores son perpendiculares.

      

   Si dos rectas son perpendiculares tienen sus pendientes inversas y cambiadas de signo.

   EJEMPLO: Calcular una recta perpendicular a r ≡ x + 2 y + 3 = 0, que pasen por el punto A(3,5).

  

TERCER FORMA DE LA ECUACIÓN LINEAL

Esta forma también recibe el nombre de FORMA REDUCIDA

Consiste en obtener a la ecuación igual a 1.

Ejemplo:

5x- 2y =6 5x /6 - 2y/6 = 6/65/6 x - 2/6 y = 1 

PENDIENTE Y ORDENADA AL ORIGEN

Utilizamos la fórmula:

Y = mx + b 

Para graficar esta forma se aplica el método ABSCISA Y ORDENADA AL ORIGEN.

FORMAS DE LA ECUACIÓN LINEAL

PUNTO - PENDIENTE

Para aplicar esta forma requerimos las coordenadas de un punto y la pendiente de la recta.

En caso de que no tengamos la pendiente se hace necesario tener 2 coordenadas que formen a esa recta.

ELEMENTOS DE UNA ECUACIÓN LINEAL O DE PRIMER GRADO

FORMA GENERAL DE UNA ECUACIÓN LINEAL:

Ax + By + C = O 

Ax = término lineal en X

By= término lineal en Y

C= término independiente

Forma pendiente ordenada el origen

Pendiente Ordenada el origen

ABSCISA Y ORDENADA EN EL ORIGEN

Existe un método para graficar a una recta que se llama ABSCISA Y ORDENADA EN EL ORIGEN
Este consiste en primer lugar en despejar cada uno de las variables.
Para poderlo hacer primeramente se le asigna a "X" el valor de 0 y posteriormente a "Y"

Tabulación de una recta

TABULACIÓN DE UNA RECTA

Una recta se puede representar mediante la construcción de una tabulación y esta transferirla a un plano cartesiano.

SIEMPRE EL LUGAR GEOMÉTRICO (GRÁFICA)  DE UNA RECTA SERÁ UNA LÍNEA.

F(X) = X
Y=X

recta

LA RECTA

Se puede definir como una sucesión de putos indefinidos que no tienen una dirección fija.

Otra manera de expresarlo es: el camino más corto entre dos puntos.

Las rectas pueden tener cualquier posición y sus ángulos de inclinación pueden ser de 0° a 360°

UNIDAD 2. LA RECTA

ANGULO DE INCLINACIÓN DE UNA RECTA

Para obtener el ángulo de inclinación de una recta es necesario primero obtener el calor de la pendiente, posteriormente ese valor se trabaja en decimales y se transfiere a la función inverso tangente de nuestra calculadora.

USO DE CALCULADORA:

SHIFT 

Tangente

el valor 

grados 

PENDIENTE DE UNA RECTA

La pendiente de una recta es considerada como la inclinación que presenta esta con respecto a un plano horizontal. Ejemplos:

Un avión al despegar se desliza a cierta velocidad sobre una pista que es nuestro plano horizontal, al obtener cierta velocidad se eleva.

A esto se le llama PENDIENTE.

OTROS EJEMPLOS:

La pendiente de un segmento de recta se puede obtener mediante el cociente de la diferencia de las ordenadas entre la diferencia de las abscisas.

TRABAJANDO VALORES: AMOR

PUNTO MEDIO DE UN SEGMENTO DE RECTA.

El punto medio es el que divide exactamente a dicho segmento en 2 partes iguales.

En geometría plana lo podemos hacer utilizando una regla o un compás.

Pero en geometría analítica cambia la situación, aquí utilizamos las siguientes formulas:

EJEMPLOS

Distancia entre dos puntos:ejemplos

Distancia entre dos puntos

DISTANCIA ENTRE DOS PUNTOS.

La distancia entre dos puntos es igual a la raíz cuadrada de la suma del cuadrado de la diferencia de las abscisas más el cuadrado de la diferencia de las abscisas más el cuadrado de la resta de las ordenadas.

Problemas fundamentales

PROBLEMAS FUNDAMENTALES DE LA GEOMETRÍA ANALÍTICA.

1.- Dado el lugar geométrico en un sistema de coordenadas obtener su ecuación.
2.-De la ecuación obtener el sistema de coordenadas.

DISTANCIA ENTRE DOS PUNTOS

VIDEOS DE APOYO - DISTANCIA ENTRE 2 PUNTOS

LOS 2 PROBLEMAS FUNDAMENTALES DE LA GEPMETRIA ANALITICA

GEOMETRIA ANALITICA

“Se conoce como geometría analítica al estudio de ciertos objetos geométricos mediante técnicas básicas del análisis matemático y del álgebra en un determinado sistema de coordenadas. Se podría decir que es el desarrollo histórico que comienza con la geometría cartesiana y concluye con la aparición de la geometría diferencial con Gauss y más tarde con el desarrollo de la geometría algebraica.

Los dos problemas fundamentales de la geometría analítica son:

1.- Dado el lugar geométrico en un sistema de coordenadas, obtener su ecuación.

2.- Dada la ecuación en un sistema de coordenadas, determinar la gráfica o lugar geométrico de los puntos que la cumplen.

PARA PODER GRAFICAR UNA ECUCIÓN DEBEMOS TOMAR LOS SIGUIENTES PUNTOS:

Intersección en los ejes:

La intersección con los ejes es el punto donde la función se interseca con los ejes "X" e "Y" (Abscisa y ordenada respectivamente).Hay una forma muy fácil de sacar la intersección con los ejes que es haciendo tender la variable "x" a cero en el caso de la intersección con el eje "Y"(ordenada) y en el caso de la intersección con el eje "X" (abscisa) hay quehacer tender el valor de la variable "Y" a cero.

EXTENSIÓN DE LA CURVA

La extensión se refiere a encontrar los valores de ´xµ y de ´yµ por medio de una tabulación es decir encontrar los valores del dominio (x) y los valores del rango o contra dominio solamente debemos seguir restricción de no aceptar divisiones entre 0 y raíces negativas.

ASÍNTOTAS

Una asíntota es una línea recta que divide a un plano y dirige a la gráfica hacia el infinito, la distancia entre una asíntota y un lugar geométrico (graficas) va tender a cero pero nunca será igual a cero.

Existen las asíntotas horizontales y verticales y las podremos localizar sial despejar ala ´yµ en el denominador hay un término de ´xµ y si al despejar a ´xµ en el dominador hay un término de ´yµ es decir que hay una división de una constante en cero.

LOCALIZACION DE PUNTOS EN EL PLANO CARTESIANO

CONCEPTOS BÁSICOS DE LA GEOMETRIA ANALITICA

Geometría: Del latín geometría, que proviene del idioma griego γεωμετρία, geo tierra y metría medida. Es una rama de la matemática que se ocupa del estudio de las propiedades de las figuras geométricas en el plano o el espacio.

Geometría Analítica. Rama de las matemáticas que une al Álgebra y a la Geometría Plana en un estudio profundo del espacio, ya sea bidimensional o tridimensional.

Recta. La recta o línea recta, se extiende en una misma dirección, existe en una sola dimensión y contiene infinitos puntos; está compuesta de infinitos segmentos. También se describe como la sucesión continua e indefinida de puntos en una sola dimensión, o sea, no posee principio ni fin.

Segmento. Es una porción finita de recta comprendida entre dos puntos llamados extremos.

Longitud es un término que deriva del vocablo latino longitūdo. Se trata de la magnitud física que expresa la distancia entre dos puntos. El Sistema Internacional establece que su unidad de longitud es el metro.

Sistema de coordenadas. Un sistema de coordenadas es un conjunto de valores y puntos que permiten definir unívocamente la posición de cualquier punto de un espacio elucídelo.

Coordenadas cartesianas. Las coordenadas cartesianas se usan por ejemplo para definir un sistema cartesiano o sistema de referencia respecto ya sea a un solo eje (línea recta), respecto a dos ejes (un plano) o respecto a tres ejes (en el espacio), perpendiculares entre sí (plano y espacio), que se cortan en un punto llamado origen de coordenadas. En el plano, las coordenadas cartesianas (o rectangulares) x e y se denominan abscisa y ordenada, respectivamente.

Distancia. Es la longitud del segmento de recta que los une dos puntos, expresado numéricamente.

Pendiente. Es la inclinación de la tangente en un punto.

Teorema de Pitágoras. Establece que en todo triángulo rectángulo el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.

Triángulo rectángulo. Es aquel en el que uno de sus ángulos es recto, es decir, mide 90°

OBJETIVOS

·           ·         Identificar las coordenadas de un punto en el plano y conocer su interpretación geométrica. ·         Reconocer y representar gráficamente lugares geométricos de puntos a distancia constante de los ejes. ·         Expresar en una tabla de valores y representar gráficamente las soluciones de una ecuación de primer grado con dos incógnitas. ·         Estudiar analíticamente la incidencia entre puntos y rectas. ·         Determinar la posición relativa entre dos rectas y, como aplicación, discutir y resolver un sistema 2x2.

Aplicaciones De La Geometría

Es la base teórica de la geometría descriptiva o del dibujo técnico. - También da fundamento a instrumentos como el compás, el teodolito, el pantógrafoo el sistema de posicionamiento global.

Aplicaciones de la geometría analítica

LA PARÁBOLA
el caso de los chorros de agua que salen de los caños de las numerosas fuentes que podemos encontrar en las ciudades.
LA HIPÉRBOLA
Estas aparecen en algunas edificaciones.
Telecomunicaciones
Antena de foco primario
Antena offset
Antena cassegrain
Antena plana

PLANO CARTESIANO

PLANO CARTESIANO

BIOGRAFÍA RENE DESCARTES

RENÉ   DESCARTES

 Nació en La Haye (Turaine; Francia) el 31 de Marzo de 1.596 y murió en Estocolmo (Suecia) el 11 de Febrero de 1.650  a causa de una afección pulmonar. Su familia pertenecía a la rica burguesía y su madre murió cuando él tenía un año de edad. Fue educado en el colegio de La Flèche, regentado por los jesuitas y considerado uno de los más famosos de Europa; allí permaneció entre 1.604 y 1.615, estudiando a los clásicos. Como curiosidad digamos que, debido a su frágil salud, en el colegio tenía permiso para permanecer en la cama hasta las 11 h. de la mañana y conservó esta costumbre el resto de su vida.

Descartes tuvo una vida muy agitada y repleta de viajes. En 1.617 se alistó como voluntario en el ejército de Mauricio de Nassau; en 1.619  en el del elector de Baviera y en 1.621, en el del conde de Bucquoy. Abandonó las armas para darse de lleno a la meditación filosófica. Viajó por Hungría, Alemania, Polonia, Países Bajos, Suiza e Italia, y de vez en cuando regresó a París, o al lado de su familia en Rennes. En 1.629 marchó a los Países Bajos, donde esperaba encontrar libertad y silencio; allí vivió unos veinte años. Mientras residía en Holanda conoció a Isaac Beeckmann, doctor holandés que apreció mucho la cultura y las notables dotes naturales del joven Descartes y, en consecuencia, le animó a reanudar los estudios, con lo cual encontró su verdadera vocación. Esta estancia fue interrumpida por un viaje a Dinamarca y tres viajes a Francia. La reina Cristina de Suecia le llamó para que fuera su profesor de filosofía. Allí en Estocolmo no pudo soportar el rigor del invierno sueco y falleció inesperadamente, víctima de una afección pulmonar, cuando sólo contaba cincuenta y cuatro años de edad.

La obra más importante de René Descartes fue El Discurso del Método (Discours de la méthod pour bien conduire la raison et chercher la vérité dans las sciences), que publicó en 1637. Dentro de esta obra, lo más destacado son tres apéndices:
 

La Dioptrique, un tratado sobre óptica que recopila las ideas         existentes entonces sobre el tema y recoge algunas aportaciones propias originales.

Les Météores, un tratado sobre meteorología.

La Géométrie, un tratado sobre geometría, que es, sin lugar a dudas, su mayor aportación a la ciencia y en concreto a las matemáticas. En este trabajo consigue establecer una sólida relación entre la geometría (prácticamente experimental entonces) y el álgebra, que caminaban por separado. Esto ha marcado el desarrollo de las Matemáticas hasta hoy, dando lugar al nacimiento de la geometría analítica (prácticamente en la línea en la que la estudiamos hoy en secundaria). Un ejemplo de la trascendencia de sus trabajos es la introducción de dos diagramas "Cartesianos" con sus coordenadas también llamadas "Cartesianas"  que reciben su nombre del propio Descartes.

Otras obras importantes: El Compendium musicae (1618); las Regulae ad directiomem ingenii (1628); el Tratado del hombre (1633); Discurso del método (la Dióptrica, los Meteoros, la Geometría) (1637); Las Meditaciones Metafísicas (1641); Los Principios Filosóficos (1644); Las Pasiones del Alma (1649); Tratado de las pasiones humanas (1650); y una extensa correspondencia con numerosos sabios, filósofos, teólogos y con la princesa Isabel de Suecia.

ACTIVIDAD 2

CURSO DE TRIGONOMETRIA

Este curso comenzó para mi aprendiendo que es un goniometro el cual es un aparato para medir ángulos, se parece a un transportador. Después investigamos de ello.
Posteriormente revisamos los tipos de triángulos. los cuales se clasifican en 3 al igual que los triángulos.
Realizamos ejercicios con los ángulos para formar 180° o 90° (suplementarios y complementarios)
Algo que también revisábamos seguido eran biografías por ejemplo Hiparco de Nicea, Herón, Euler, Pitágoras, etc
También realizamos ejercicios con la recta de Euler identificando la mediatriz, bisectriz, varicentro, circuncentro
Realizamos problemas que incluyeran ángulos 
Vimos el valor exacto del seno, coseno y tangente
Revisamos:
-Funciones Trigonométricas
-Uso de calculadora científica para identificar funciones trigonométricas
-Uso de calculadora para tabular
-Problemas de funciones trigonométricas
-También realizamos problemas de encontrar X
También revisamos los radianes y como convertir de grados a radianes y de radianes a grados